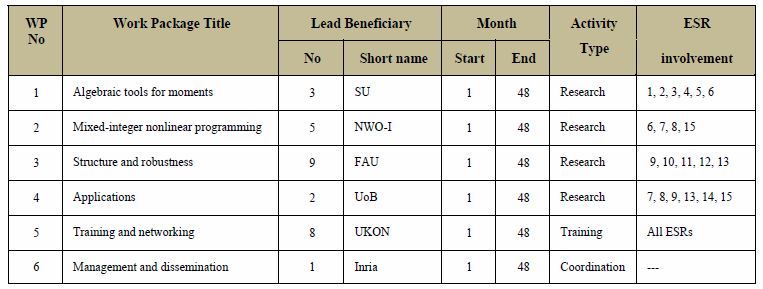
To efficiently ensure the training of young researcher on the State-of-the-Art Mathematical optimization, POEMA has been structured around six work-packages
WP1 concerns algebraic tools for moments and sums of squares problems. The formulation of Polynomial Optimization Problems as moment problems allows exploiting algebraic tools for the development of efficient solvers. Classical algebraic techniques for manipulating polynomial equations and semi-algebraic sets, such as Cylindrical Algebraic Decomposition and Gröbner Basis computation, are being enriched by duality tools from moment problems. This opens up new perspectives for computing efficiently the real solutions of polynomial problems
WP2 is dedicated to mixed-integer nonlinear programming and to semidefinite programming for problems that combine continuous and discrete variables. We intend to study hierarchies of semidefinite programmingbased approximations of combinatorial optimization problems such as those related to graphs. We will also investigate these questions within the more general framework of non-commutative polynomial algebra, since non-commutative polynomial optimization problems arise naturally, for instance, in quantum information and
WP3 is dedicated to analyse and exploit the structure that appears in polynomial optimization problems in order to improve the performance of the Semidefinite Programming solvers and the numerical quality of their solution. Sparsity, symmetry, separable variables are structures that should be open to exploitation in order to improve the performance of the Semidefinite Programming solvers and the numerical quality of their solution. It is envisaged that reduction techniques and basis transformations will be used to produce SDP relaxations of smaller size and better numerical behaviour.
WP4 is dedicated to challenging decision optimization problems arising from applications in environment, urban networks, biology, mechanics and finance. Specific optimization problems such as power network management, water consumption, genome reconstruction and mechanism optimization, and portfolio optimization will be studied. It aims to demonstrate the potential of polynomial optimization to find better solutions to industrial decision optimization problems and to solve novel practical decision optimization problems. The methods and tools developed in the previous work-packages will be confronted to practical problems, in order to validate and improve the research results, leading to a strong interplay between theoretical approaches and real life problems.
WP5 dedicated to training, and coordinated by work-package WP6 focusing on management and dissemination of the network activities.